SOAL TRIGONOMETRI MATEMATIKA

Tugas Soal Tanggal 4-5 Mei

3.7 Menyelesaikan cara merubah satuan pengukuran sudut trigonometri radian ke derajat, derajat ke radian

Soal :
1.Ubahlah  sudut-sudut berikut dalam derajat
a.  $\frac{\pi }{3}$ rad = ... °
b.  4π rad = ... °

 Jawab :
a.  $\frac{\pi }{3}$ rad  =  $\frac{\pi }{3}$ . $\frac{{180}^{\circ }}{\pi }$  =  60°
b.  4π rad  =  4π . $\frac{{180}^{\circ }}{\pi }$  =  720°

 3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku dan dudut istimewa (60⁰ , 30⁰ , 45⁰ )

soal : 1.

Pada gambar di samping segitiga siku-siku ABC dengan panjang a=8 dan c= 10.

Tentukan keenam perbandingan trigonometri untuk a.

Penyelesaian:

Nilai b dihitung dengan teorema Pythagoras

         

3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku di dalam koordinat kartesius

soal :

1. Besar sudut yang sesuai dengan gambar di bawah adalah $\cdots \cdot$

 
 Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni $-{30}^{\circ }$.
Karena satu putaran sama dengan ${360}^{\circ }$, maka $-{30}^{\circ }$ sama dengan $(360-30{)}^{\circ }={330}^{\circ }$
Jadi, besar sudutnya adalah ${330}^{\circ }$

3.7 Menyelesaikan nilai trigonometri pada suatu sudut segitiga siku-siku pada koordinat cartesius

soal :

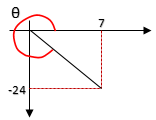
1. Perhatikan gambar dibawah! $Cos\theta =$ . . . .

$\mathrm{jawab\; :}$

3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran 
 soal :
1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20°
tan 40°
cos 53°
Jawab :
sin 20° = sin (90° − 70°)
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50°
cos 53° = cos (90° − 37°)
= sin 37°

3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut berelasi (kuadrat: I, II, III, IV), sudut negatif, dan sudut > 360⁰ 
 soal :

Nyatakan setiap perbandingan trigonometri berikut dalam sudut 37° !

tan 143°
sin 233°
cos 323°

Jawab :
Sudut 143° terletak pada kuadran II, sehingga tan 143° bernilai negatif.
tan 143° = tan (180° − 37°)
tan 143° = -tan 37°

Sudut 233° terletak pada kuadran III, sehingga sinus bernilai negatif.
sin 233° = sin (270° − 37°)
tan 233° = -cos 37°
Perhatikan bahwa sin berubah menjadi cos karena relasi yang digunakan (270° −  α)

Sudut 323° terletak pada kuadran IV, sehingga cosinus bernilai positif.
cos 323° = cos (360° − 37°)
cos 323° = cos 37°

3.8 Menyelesaikan persamaan trigonometri sederhana atau persamaan indentitas trigonometri = rumus identitas trigonometri

soal :

 1. Apabila tan 9°= p. Tentukanlah nilai dari tan 54°

Jawaban:
tan 54° = tan (45° + 9°)
= tan 45° + tan 9°/1 – tan 45° x tan 9°
= 1 + p/1 – p

Sehingga, hasil nilai dari tan 54° adalah = 1 + p/1 – p

 3.8 Menyelesaikan Koordinat kutub ke koordinat kartesius, koordinat kartesius ke koordinat kutub

 soal :

1. Konversikan koordinat kartesius P (4,-3) menjadi koordinat kutub!

Penyelesaian:
Diketahui:  x = 4 dan y = -3

maka r = √x²+y² = √4²+(-3)² = √25 = 5

           α = tan^-1 (y/x) = tan^-1 (-3/4)
              = -36,69 ° atau -37°
Jadi koordinat kutubnya (5, -37°).

3.9 Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi

soal :

1. Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besardan, maka panjang BC = … cm.

Pembahasan:

Berdasarkan informasi yang diberikan pada soal, dapat diperoleh informasi seperti berikut ini.

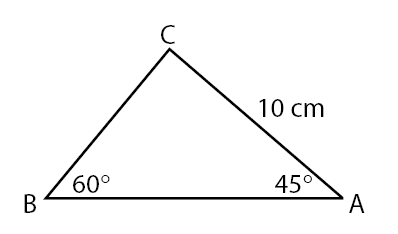
Panjang BC dapat dicari menggunakan aturan sinus.

   

   

   

   

   

   

   

3.9 Menyelesaikan aturan cos ditanya sisi
soal :

1. Diketahui sebuah segitiga ABC memiliki sisi dengan panjang
a = 10 cm
c = 12 cm
besar sudut B = 60̊.
Hitung panjang sisi b!

Pembahasan

b² = a²+ c² – 2ac cos B
b² = 100+144 – 44 cos 60̊
b² = 244 – 44(0,5)
b² = 244 – 22
b² = 222
b = 14,8997
Jadi, panjang sisi b adalah 14,8997 cm
 3.9 Menyelesaikan aturan cos ditanya sudut
soal :

Diberikan segitiga ABC seperti gambar berikut ini



AB = 20 cm, BC = 10√3 cm dan AC = 10 cm. Tentukan besar ∠A 

Pembahasan
Data segitiga:
a = 10√3 cm
b = 10 cm
c = 20 cm
∠A =.... 

Dengan aturan kosinus pada ΔABC diperoleh nilai sudut A:



Sudut yang memiliki nilai cos sama dengan 1/2 adalah 60° 
 3.10 Menyelesaikan gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
soal :
Jika f ‘(x) merupakan turunan dari f(x) dan jika f(x) = ( 3x – 2 ) sin (2x + 1) maka f ‘ (x) adalah …

• 3 cos( 2x + 1 )
• 6 cos( 2x + 1 )
• 3 sin( 2 x + 1 ) + (6 x – 4) cos (2 x + 1)
• (6x –4) sin ( 2x + 1 ) + 3 cos ( 2x + 1 )
• E. 3 sin( 2x + 1) + ( 3x – 2 ) cos( 2x + 1 ).

Jawab ;

 kita misalkan terlebih dahulu

ingat rumus turunan perkalian dua fungsi ;

3.7 Menyelesaikan sudut elevasi, sudut depresi

soal :

3.10 Menyelesaikan fungsi trigonometri dengan menggunakan lingkaran satuan untuk menentukan periode maksimum dan minimum

soal :

 1). Tentukan nilai maksimum dari fungsi f(x)=−x2+4x+3 ?

Penyelesaian : 
*). Fungsi awal : f(x)=−x2+4x+3 
f′(x)=−2x+4 dan f′′(x)=−2 
*). Menentukan nilai x dari syarat stasioner : f′(x)=0 
f′(x)=0→−2x+4=0→x=2 . 
*). Menentukan jenis stasionernya : gunakan turunan kedua. 
untuk x=4→f′′(2)=−2 (negatif), jenisnya maksimum. Artinya nilai x=2 menyebabkan fungsinya maksimum. 
*). Menentukan nilai maksimum saat x=2 , substitusi ke fungsi awal 
fmaks=f(2)=−(2)2+4.2+3=7 
Jadi, nilai maksimum fungsi f(x)=−x2+4x+3 adalah 7 pada saat x=2 . 

2). Tentukan nilai minimum fungsi f(x)=13x3+12x2−2x+3 ? 
Penyelesaian : 
*). Fungsi awal : f(x)=13x3+12x2−2x+3 
f′(x)=x2+x−2 dan f′′(x)=2x+1 
*). Menentukan nilai x dari syarat stasioner : f′(x)=0 
f′(x)=0→x2+x−2=0→(x+2)(x−1)=0→x=−2∨x=1. 
*). Menentukan jenis stasionernya : gunakan turunan kedua. 
untuk x=−2→f′′(−2)=2.(−2)+1=−3 (negatif), jenisnya maksimum. Artinya nilai x=−2 menyebabkan fungsinya maksimum. 
untuk x=1→f′′(1)=2.(1)+1=3 (positif), jenisnya minimum. Artinya nilai x=1 menyebabkan fungsinya minimum. 
*). Menentukan nilai minimum saat x=1 , substitusi ke fungsi awal 
fmin=f(1)=13.13+12.12−2.1+3=116 
Jadi, nilai maksimum fungsi f(x)=13x3+12x2−2x+3 adalah 116 pada saat x=1 .