"Pengalaman Belajar Matematika dan soal Trigonometri" Reinaldi Akmal(31) X IPS 2

 Assalamualaikum wr.wb,

Perkenalkan , Saya Reinaldi Akmal absen (31) Kelas X IPS 2 dari SMAN 63 Jakarta Selatan.

Tujuan pembuatan blog ini adalah untuk memenuhi tugas Matematika Pada hari selasa,28,april,2020.

Puji dan Syukur kita panjatkan atas kehadirat ALLAH SWT. yang selalu memberikan kesehatan kepada kita sampai saat ini.

            Pengalaman belajar Matematika SMAN 63 Jakarta Selatan,Oleh Reinaldi Akmal (31) X IPS 2 , Menurut Saya dalam pembelajaran matematika di semester 2 ini cukup sulit namun seiring waktu saya dapat mengikuti materinya dengan cukup baik. Dalam keadaan PSBB ini kegiatan KBM yang awalnya dilaksanakan disekolah mulai diganti sementara menjadi PJJ dirumah, meski banyak kendala dalam pembelajaran jarak jauh ini tapi saya selalu berusaha mengerjakan tugas yang diberikan tepat waktu.

            Salah satu pembelajaran yang saya sukai adalah pada saat pengerjaan tugas. saya merasa dapat menjadi lebih rajin dan mandiri dalam belajar meski terkadang harus dibantu oleh teman yang lebih ahli.Selain itu PJJ yang saya sukai adalah saat mengerjakan schoology tentang kaitan virus corona dengan matematika menurut saya itu adalah hal yang menarik bahwasanya pelajaran matematika dapat menjadi sarana penghitungan untuk wabah virus corona. 

sekian cerita pengalaman saya, mohon maaf bila ada salah pengetikan. terakhir terimakasih assalamualaikum wr.wb

Tugas Soal Tanggal 4-5 Mei

3.7 Menyelesaikan cara merubah satuan pengukuran sudut trigonometri radian ke derajat, derajat ke radian

Soal :
1.Ubahlah  sudut-sudut berikut dalam derajat
a.  $\frac{\pi }{3}$ rad = ... °
b.  4π rad = ... °

 Jawab :
a.  $\frac{\pi }{3}$ rad  =  $\frac{\pi }{3}$ . $\frac{{180}^{\circ }}{\pi }$  =  60°
b.  4π rad  =  4π . $\frac{{180}^{\circ }}{\pi }$  =  720°

 3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku dan dudut istimewa (60⁰ , 30⁰ , 45⁰ )

soal : 1.

Pada gambar di samping segitiga siku-siku ABC dengan panjang a=8 dan c= 10.

Tentukan keenam perbandingan trigonometri untuk a.

Penyelesaian:

Nilai b dihitung dengan teorema Pythagoras

         

3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku di dalam koordinat kartesius

soal :

1. Besar sudut yang sesuai dengan gambar di bawah adalah $\cdots \cdot$

 
 Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni $-{30}^{\circ }$.
Karena satu putaran sama dengan ${360}^{\circ }$, maka $-{30}^{\circ }$ sama dengan $(360-30{)}^{\circ }={330}^{\circ }$
Jadi, besar sudutnya adalah ${330}^{\circ }$

3.7 Menyelesaikan nilai trigonometri pada suatu sudut segitiga siku-siku pada koordinat cartesius

soal :

1. Perhatikan gambar dibawah! $Cos\theta =$ . . . .

$\mathrm{jawab\; :}$

$\mathrm{x=7,\; y=-24,\; r=25\; (Phytagoras)\; Koordinat\; Cartesius\; \to \; cos=absis/radius}$

$\mathrm{cos\theta \; =x/r=725}$

3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran
 soal :
1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20°
tan 40°
cos 53°
Jawab :
sin 20° = sin (90° − 70°)
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50°
cos 53° = cos (90° − 37°)
= sin 37°

3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut berelasi (kuadrat: I, II, III, IV), sudut negatif, dan sudut > 360⁰
 soal :

$\mathrm{1.}$Nyatakan setiap perbandingan trigonometri berikut dalam sudut 37° !

tan 143°
sin 233°
cos 323°

Jawab :
Sudut 143° terletak pada kuadran II, sehingga tan 143° bernilai negatif.
tan 143° = tan (180° − 37°)
tan 143° = -tan 37°

Sudut 233° terletak pada kuadran III, sehingga sinus bernilai negatif.
sin 233° = sin (270° − 37°)
tan 233° = -cos 37°
Perhatikan bahwa sin berubah menjadi cos karena relasi yang digunakan (270° −  α)

Sudut 323° terletak pada kuadran IV, sehingga cosinus bernilai positif.
cos 323° = cos (360° − 37°)
cos 323° = cos 37°

3.8 Menyelesaikan persamaan trigonometri sederhana atau persamaan indentitas trigonometri = rumus identitas trigonometri

soal :

 1. Apabila tan 9°= p. Tentukanlah nilai dari tan 54°

Jawaban:
tan 54° = tan (45° + 9°)
= tan 45° + tan 9°/1 – tan 45° x tan 9°
= 1 + p/1 – p

Sehingga, hasil nilai dari tan 54° adalah = 1 + p/1 – p

 3.8 Menyelesaikan Koordinat kutub ke koordinat kartesius, koordinat kartesius ke koordinat kutub

 soal :

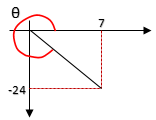
1. Konversikan koordinat kartesius P (4,-3) menjadi koordinat kutub!

Penyelesaian:
Diketahui:  x = 4 dan y = -3

maka r = √x²+y² = √4²+(-3)² = √25 = 5

           α = tan^-1 (y/x) = tan^-1 (-3/4)
              = -36,69 ° atau -37°
Jadi koordinat kutubnya (5, -37°).

3.9 Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi

soal :

1. Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar dan , maka panjang BC = … cm.

Pembahasan: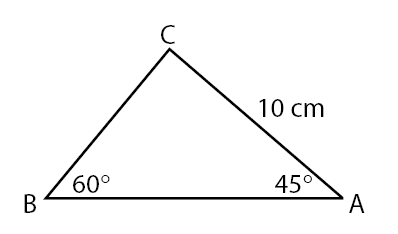

Berdasarkan informasi yang diberikan pada soal, dapat diperoleh informasi seperti berikut ini.

Panjang BC dapat dicari menggunakan aturan sinus.

   

   

   

   

   

   

   

3.9 Menyelesaikan aturan cos ditanya sisi
soal :

1. Diketahui sebuah segitiga ABC memiliki sisi dengan panjang
a = 10 cm
c = 12 cm
besar sudut B = 60̊.
Hitung panjang sisi b!

Pembahasan

b² = a²+ c² – 2ac cos B
b² = 100+144 – 44 cos 60̊
b² = 244 – 44(0,5)
b² = 244 – 22
b² = 222
b = 14,8997
Jadi, panjang sisi b adalah 14,8997 cm
 3.9 Menyelesaikan aturan cos ditanya sudut
soal :

Diberikan segitiga ABC seperti gambar berikut ini



AB = 20 cm, BC = 10√3 cm dan AC = 10 cm. Tentukan besar ∠A

Pembahasan
Data segitiga:
a = 10√3 cm
b = 10 cm
c = 20 cm
∠A =....

Dengan aturan kosinus pada ΔABC diperoleh nilai sudut A:



Sudut yang memiliki nilai cos sama dengan 1/2 adalah 60° 
 3.10 Menyelesaikan gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
soal :
Jika f ‘(x) merupakan turunan dari f(x) dan jika f(x) = ( 3x – 2 ) sin (2x + 1) maka f ‘ (x) adalah …

• 3 cos( 2x + 1 )
• 6 cos( 2x + 1 )
• 3 sin( 2 x + 1 ) + (6 x – 4) cos (2 x + 1)
• (6x –4) sin ( 2x + 1 ) + 3 cos ( 2x + 1 )
• E. 3 sin( 2x + 1) + ( 3x – 2 ) cos( 2x + 1 ).

Jawab ;

 kita misalkan terlebih dahulu

ingat rumus turunan perkalian dua fungsi ;

3.7 Menyelesaikan sudut elevasi, sudut depresi

soal :

3.10 Menyelesaikan fungsi trigonometri dengan menggunakan lingkaran satuan untuk menentukan periode maksimum dan minimum

soal :

 1). Tentukan nilai maksimum dari fungsi f(x)=−x2+4x+3 ?

Penyelesaian :
*). Fungsi awal : f(x)=−x2+4x+3
f′(x)=−2x+4 dan f′′(x)=−2
*). Menentukan nilai x dari syarat stasioner : f′(x)=0
f′(x)=0→−2x+4=0→x=2 .
*). Menentukan jenis stasionernya : gunakan turunan kedua.
untuk x=4→f′′(2)=−2 (negatif), jenisnya maksimum. Artinya nilai x=2 menyebabkan fungsinya maksimum.
*). Menentukan nilai maksimum saat x=2 , substitusi ke fungsi awal
fmaks=f(2)=−(2)2+4.2+3=7
Jadi, nilai maksimum fungsi f(x)=−x2+4x+3 adalah 7 pada saat x=2 .

2). Tentukan nilai minimum fungsi f(x)=13x3+12x2−2x+3 ?
Penyelesaian :
*). Fungsi awal : f(x)=13x3+12x2−2x+3
f′(x)=x2+x−2 dan f′′(x)=2x+1
*). Menentukan nilai x dari syarat stasioner : f′(x)=0
f′(x)=0→x2+x−2=0→(x+2)(x−1)=0→x=−2∨x=1 .
*). Menentukan jenis stasionernya : gunakan turunan kedua.
untuk x=−2→f′′(−2)=2.(−2)+1=−3 (negatif), jenisnya maksimum. Artinya nilai x=−2 menyebabkan fungsinya maksimum.
untuk x=1→f′′(1)=2.(1)+1=3 (positif), jenisnya minimum. Artinya nilai x=1 menyebabkan fungsinya minimum.
*). Menentukan nilai minimum saat x=1 , substitusi ke fungsi awal
fmin=f(1)=13.13+12.12−2.1+3=116
Jadi, nilai maksimum fungsi f(x)=13x3+12x2−2x+3 adalah 116 pada saat x=1 .