Menggambar grafik fungsi dengan Turunan
Nama : Reinaldi Akmal (30)
Kelas : XI IPS 2
Contoh soal fungsi kuadrat dan pembahasannya + Jawaban
- Jika a > 0 dan D > 0, grafik fungsi kuadrat memotong sumbu X di dua titik yang berbeda. Jenis titik baliknya minimum.
- Jika a > 0 dan D = 0, grafik fungsi kuadrat memotong sumbu X di satu titik atau menyinggung sumbu X. Jenis titik baliknya minimum.
- Jika a > 0 dan D < 0, grafik fungsi kuadrat tidak memotong sumbu X (definit positif). Jenis titik baliknya minimum.
- Jika a < 0 dan D > 0, grafik fungsi kuadrat memotong sumbu X di dua titik berbeda. Jenis titik baliknya maksimum.
- Jika a < 0 dan D = 0, grafik fungsi kuadrat menyinggung sumbu X dan titik baliknya maksimum.
- Jika a < 0 dan D < 0, grafik fungsi kuadrat tidak memotong sumbu X (definit negatif) dan titik balinya maksimum.

Rumus yang berlaku pada fungsi kuadrat sebagai berikut.

Contoh soal fungsi kuadrat
Contoh soal 1
Gambarkanlah grafik fungsi kuadrat f(x) = x2 + 4x – 21 pada himpunan bilangan nyata.
Pembahasan / penyelesaian soal
Cara menggambar grafik fungsi kuadrat sebagai berikut:
Menentukan titik potong sumbu x dengan cara pemfaktoran:x2 + 4x – 21 = 0
(x1 + 7) (x2 – 3) = 0
x1 = -7 dam x2 = 3
Titik potong pada sumbu X adalah A(-7 ; 0) dan B ((3 ; 0)
Menentukan titik potong sumbu Y dengan subtitusi x = 0 atau f(0)
f(x) = x2 + 4x – 21
f(0) = 02 + 4 . 0 – 21 = -21
Jadi titik potong sumbu Y adalah (0 ; -21)
Menentukan titik balik (xp , yp) dengan rumus dibawah ini:
xp = -b -4
yp = – (42 – 4 . 1 . -21)
Dengan demikian gambar grafik kuadrat soal nomor 1 sebagai berikut:

Contoh soal 2
Tentukan persamaan sumbu simetri grafik fungsi kuadrat sebagai berikut:
- y = 8x2 + 6x – 9
- y = x2 + 7x – 8
Pembahasan / penyelesaian soal
- a = 8, b = 6 dan c = -9 sehingga persamaan sumbu simetri x = – b/2a = – 6 / (2 . 8) = – 6/16 = – 3/8
- a = 1, b = 7 dan c = -8 sehingga persamaan sumbu simetri x = -b/2a = – 7 / (2 . 1) = – 7/2
Contoh soal 3
Selidikilah apakah grafik fungsi berikut memotong sumbu X, menyinggung sumbu X atau tidak memotong sumbu X.
- y = x2 + 9x + 20
- y = 2x2 – 3x + 1
Pembahasan / penyelesaian soal
- a = 1 dan D = b2 – 4ac = 92 – 4 . 1 . 20 = 81 – 80 = 1. Karena a > 0 dan D > 0 maka grafik fungsi kuadrat memotong sumbu X.
- a = 2 dan D = b2 – 4ac = -32 – 4 . 2 . 1 = 9 – 8 = 1. Karena a > 0 dan D > 0 maka grafik fungsi kuadrat memotong sumbu X.
Contoh soal 4
Selidiki apakah fungsi kuadrat dibawah ini tergolong definit positif, definit negatif atau bukan keduanya.
- y = 3x2 – 4x – 2
- y = 4x2 – 3x + 5
Pembahasan / penyelesaian soal
Definit positif jika a > 0 dan D < 0 sedangkan definit negatif jika a < 0 dan D < 0.
- a = 3 dan D = b2 – 4ac = (-4)2 – 4 . 3 . -2 = 16 + 24 = 40. Karena a > 0 dan D > 0 maka fungsi kuadrat bukan definit positif dan bukan definit negatif (bukan keduanya).
- a = 1 dan D = b2 – 4ac = (-3)2 – 4 . 4 . 5 = 9 – 80 = – 71. Karena a > 0 dan D < 0 maka fungsi kuadrat definit positif.
Contoh soal 5
Perhatikan gambar fungsi kuadrat dibawah ini.

Persamaan fungsi kuadrat grafik diatas adalah…
A. y = x2 – 2x + 15
B. y = x2 – 2x – 15
C. y = x2 + 2x + 15
D. y = x2 – 8x – 15
E. y = x2 – 8x + 15
Pembahasan / penyelesaian soal
Berdasarkan grafik fungsi kuadrat diatas kita ketahui:
- x1 = -5
- x2 = -3
- y = 15
Fungsi kuadrat dibentuk dengan cara sebagai berikut:
- y = a (x – x1) (x – x2)
- y = a (x – (-5)) (x – (-3))
- y = a (x + 5) (x + 3)
- y = a (x2 + 3x + 5 x + 15)
- y = a (x2 + 8x + 15)
Selanjutnya kita tentukan nilai a dengan subtitusi nilai x = 0 dan y = 15 sehingga didapat:
- 15 = a (02 + 8 . 0 + 15)
- 15 = a . 15
- a = 15/15 = 1
Jadi fungsi kuadratnya adalah:
- y = 1 (x2 + 8x + 15)
- y = x2 + 8x + 15
Jadi soal ini jawabannya C.
Contoh soal 6

Persamaan fungsi kuadrat grafik diatas adalah…
A. y = 2x2 + 2x – 4
B. y = 2x2 – 2x – 4
C. y = x2 + x – 4
D. y = x2 – 2x – 4
E. y = x2 – x – 4
Pembahasan / penyelesaian soal
Berdasarkan grafik diatas kita ketahui:
- x1 = -1
- x2 = 2
- y = -4
Maka persamaan fungsi kuadrat sebagai berikut:
- y = a (x – (-1)) (x – 2)
- y = a (x + 1) (x – 2)
- y = a (x2 – x – 2)
Menentukan nilai a dengan cara subtitusi x = 0 dan y = -4 sehingga didapat hasil dibawah ini:
- -4 = a (02 – 0 – 2)
- -4 = a . -2
- a = -4/-2 = 2
Sehingga persamaan kuadratnya adalah:
- y = 2 (x2 – x – 2)
- y = 2x2 – 2x – 4
Soal ini jawabannya B.
Contoh soal 7
Perhatikan gambar dibawah ini.
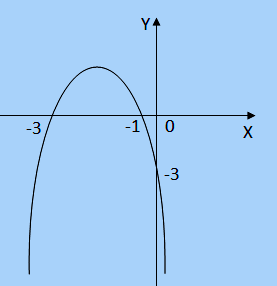
Jika fungsi kuadrat grafik diatas dinyatakan oleh f(x) = ax2 + bx + c maka pernyataan dibawah ini yang benar adalah…
A. a < 0, b < 0, dan c < 0
B. a < 0, b > 0 dan c > 0
C. a < 0, b > 0 dan c < 0
D. a > 0, b < 0 dan c > 0
E. a > 0, b < 0 dan c < 0
Pembahasan / penyelesaian soal
Untuk menjawab soal ini kita bentuk terlebih dahulu persamaan fungsi kuadrat grafik diatas sebagai berikut:
- y = a (x – (-3)) (x – (-1))
- y = a (x + 3) (x + 1)
- y = a (x2 + 4x + 3)
- -3 = a (02 + 4 . 0 + 3)
- -3 = a . 3
- a = -3/3 = -1
- y = -1 (x2 + 4x + 3)
- y = -x2 – 4x – 3
Berdasarkan persamaan fungsi kuadrat diatas kita ketahui a = -1, b = -4 dan c = -3 atau a < 0, b < 0 dan c < 0. Jadi jawaban soal ini adalah A.
Contoh soal 8
Perhatikan gambar dibawah ini.

Koordinat titik potong grafik dengan sumbu X adalah…
A. (-1, 0) dan (-8, 0)
B. (-1, 0) dan (8, 0)
C. (1, 0) dan (-8, 0)
D. (1, 0) dan (8, 0)
E. (2, 0) dan (5, 0)
Pembahasan / penyelesaian soal
Berdasarkan grafik fungsi kuadrat diatas kita ketahui:
- titik balik xp = 9/2
- titik balik yp = -49/4
- y = 8
Sehingga kita dapat a = 2
b2 – 4 . a . c = 49
92 – 4 . 1 . c = 49
81 – 4c = 49 atau 4c = 81 – 49 = 32
c = 32
y = ax2 + bx + c
y = xp – 9x + c
Untuk menentukan titik potong x kita lakukan pemfaktoran sebagai berikut:
xp – 9x + 8 = 0
(x1 – 8) (x2 – 1) = 0
x1 = 8 dan x2 = 1
Jadi titik potong sumbu X adalah (8,0) dan (1,0). Soal ini jawabannya D.
Contoh soal 9
Diketahui jumlah 2 bilangan adalah 72. Hasil kali maksimum kedua bilangan adalah…
A. 72
B. 144
C. 360
D. 1.296
E. 5.184
Pembahasan / penyelesaian soal
Untuk menjawab soal ini kita lalukan pemisalan 2 bilangan yaitu x dan y sehingga kita peroleh:
- x + y = 72
- y = 72 – x
- x . y = x (72 – x) = 72x – x2
- K = -x2 + 72x
Berdasarkan fungsi kuadrat diatas kita ketahui a = -1, b = 72 dan c = 0. Hasil kali maksimum kita gunakan rumus dibawah ini:
Jadi soal ini jawabannya D.
K = -(b2 – 4 . a . c)K = -(722 – 4 . -1 . 0)
Jadi soal ini jawabannya D.
Contoh soal 10
Dua bilangan selisihnya 30. Agar hasil kalinya minimum maka kedua bilangan tersebut adalah…
A. 15 dan -15
B. 20 dan -10
C. 25 dan -5
D. 40 dan 10
E. 50 dan 20
Pembahasan / penyelesaian soal
Kita misalkan kedua bilangan tersebut x dan y maka kita peroleh:
- x – y = 30
- y = x – 30
- K = x . y = x . (x – 30) = x2 – 30x
Berdasarkan fungsi kuadrat diatas kita ketahui a = 1, b = -30 dan c = 0. Maka untuk menentukan nilai minimum kita gunakan rumus dibawah ini.
K = -(b2 – 4 . a . c)K = -(-302 – 4 . 1 . 0)
K = -225 dan K = x2 – 30x maka kita dapat:
x2 – 30 x = -225x2 – 30x + 225 = 0
(x – 15)2 = 0
x = 15
Kita subtitusi x = 15 ke persamaan y = x – 30 maka kita peroleh y = 15 – 30 = -15. Jadi hasil perkalian minimum jika kedua bilangan tersebut adalah 15 dan -15.
Jadi soal ini jawabannya A.
Contoh soal 11
Diketahui persegipanjang dengan keliling 64 cm. Agar luas persegi panjang maksimum maka besar panjang dan lebarnya adalah…
A. 64 cm dan 1 cm
B. 32 cm dan 2 cm
C. 32 cm dan 4 cm
D. 16 cm dan 16 cm
E. 16 cm dan 8 cm
Pembahasan / penyelesaian soal
Untuk menyelesaikan soal ini kita misalkan panjang = P dan lebar = L maka kita peroleh:
- 2 (P + L) = 64
- P + L = 32
- P = 32 – L
- Luas = P . L = (32 – L) . L = 32 L – L2
- Luas = L2 – 32L
Dari fungsi kuadrat luas diatas kita ketahui a = 1, b = -32 dan c = 0. Selanjutnya kita menentukan luas maksimum dengan cara dibawah ini:
Luas =Luas =
Luas = -256 dan Luas = L2 – 32L sehingga kita peroleh hubungan sebagai berikut:
- L2 – 32L = – 256
- L2 – 32L + 256 = 0
- (L – 16)2 = 0
- L = 16
L = 16 kita subtitusi ke persamaan L + P = 32 maka P = 32 – L = 32 – 16 = 16. Jadi panjang dan lebar persegi panjang agar maksimum adalah P = 16 cm dan L = 16 cm. Jadi soal ini jawabannya D.
DAFTAR PUSTAKA
https://soalfismat.com/contoh-soal-fungsi-kuadrat-dan-pembahasannya/


Komentar
Posting Komentar