SOAL PENYELESAIAN MENGGUNAKAN MATRIKS

-

NAMA : REINALDI AKMAL

KELAS : XI IPS 2

ABSEN : 29

 

*SOAL PENYELESAIAN MENGGUNAKAN MATRIKS

 

 A. SOAL DETERMINAN MATRIKS BERORDO 3 X 3 DAN 2 X 2

 

1. Determinan Matriks Ordo 2 x 2 :

Apabila matriksnya berbentuk 2 x 2, maka rumus untuk mencari determinan ialah :

Rumus untuk mencari determinan 2 x 2
Rumus untuk mencari determinan 2 x 2.

Nilai determinan A di simbolkan dengan | A | , cara menghitung nilai determinan A dapat di lihat seperti cara yang di bawah ini :

 Contoh soal :

1. Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

Jawaban untuk matriks ordo 2 x 2 di atas ialah seperti berikut ini :

 

 

 

 2. Determinan matriks ordo 3 x 3 :

Matriks Ordo 3 ialah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 yakni seperti cara yang di bawah ini :

Bentuk umum matriks ordo 3 x 3
Bentuk umum matriks ordo 3 x 3

Apabila matriksnya berbentuk 3 x 3 matrix A, maka rumus untuk mencari determinan ialah :

Rumus untuk mencari determinan 3 x 3 Rumus untuk mencari determinan 3  

 

 Contoh soal : 


1. Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

Jawaban untuk matriks ordo 3 x 3 di atas ialah seperti berikut ini :

det( A ) = ( 2 . 4 . 1 ) + ( 3 . 3 . 7 ) + ( 4 . 5 . 0  ) – ( 4 . 4 . 7  ) – ( 2 . 3 . 0 ) – ( 3 . 5 . 1 ) 
               =      ( 8 )       +    ( 63 )     +       ( 0 )       –     ( 112 )     –      ( 0 )       –     15
               = – 56

 

 B. SOAL KOFAKTOR MATRIKS BERORDO  3 X 3 DAN 2 X 2

 

1. Kofaktor  matriks ordo 2 x 2 :

 Contoh soal :

Tentukanlah kofaktor dari matriks

A=\begin{bmatrix}2&4\\3&5\end{bmatrix}

Jawab :

Terlebih dulu kita cari minor dari matriks A tersebut. Disini minor dari matriks A di dapat :

M_{A}=\begin{bmatrix}5&3\\4&2\end{bmatrix}

Kemudian kita cari kofaktor tiap elemen dari minor tersebut :

 ofaktor Matriks A baris pertama kolom pertama, berarti i = 1 dan j = 1.

K_{11}=(-1)^{i+j}. M_{ij}

K_{11}=(-1)^{1+1}. M_{11}

K_{11}=(-1)^{2}.5

K_{11}=1.5=5

Kofaktor matriks A baris pertama kolom kedua, berarti i = 1 dan j = 2.

K_{12}=(-1)^{1+2}.M_{12}

K_{12}=(-1)^{3}.M_{12}

K_{12}=(-1).3=-3

Kofaktor matriks A baris kedua kolom pertama, berarti i = 2 dan j = 1

K_{21}=(-1)^{2+1}.M_{21}

K_{21}=(-1)^{3}.4

K_{21}=-4

Kofaktor matriks A baris kedua kolom kedua, berarti i = 2 dan j = 2

K_{22}=(-1)^{2+2}.M_{22}

K_{22}=1.2=2

Jadi, kofaktor dari matriks A adalah

K_{A}=\begin{bmatrix}5&-3\\-4&2\end{bmatrix}

 

2. Kofaktor matriks ordo 3 x 3 :

 Contoh soal :

1. Tentukanlah Kofaktor dari matriks berikut :

A=\begin{bmatrix}2&4&6\\1&3&2\\0&1&2\end{bmatrix}

Penyelesaian :

Terlebih dahulu kita cari minor matriks A, disini didapat bahwa minor matriks A adalah :

A=\begin{bmatrix}4&0&1\\2&4&2\\10&-2&2\end{bmatrix}

Sehingga kofaktor matriks A adalah :

A=\begin{bmatrix}4&0&1\\-2&4&-2\\10&2&2\end{bmatrix}


 C. SOAL INVERS MATRIKS BERORDO 3 X 3 DAN 2 X 2

 

1. Invers matriks ordo 2 x 2 :

 

 Contoh soal :


1. Menentukan matriks invers dari!

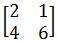
contoh soal invers matriks

Jawaban :

Untuk menghitung kebalikan dari matriks, metode cepat digunakan. Sebelum menggunakan rumus matriks terbalik di atas. Pertama-tama kita harus menemukan nilai adjoin dahulu.

Untuk menemukan matriks invers 2×2 yang berdekatan, kita hanya perlu menukar atau memindahkan elemen yang posisinya ada di baris pertama kolom pertama dengan elemen-elemen di baris kedua kolom kedua.

Berikutnya, baris kedua dari kolom pertama dan baris pertama dari kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.

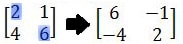
jawaban soal invers matriks

Selanjutnya, cari determinan matriks
det = (2 × 6) – (4 × 1)
= 12 – 4
= 8

Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah :

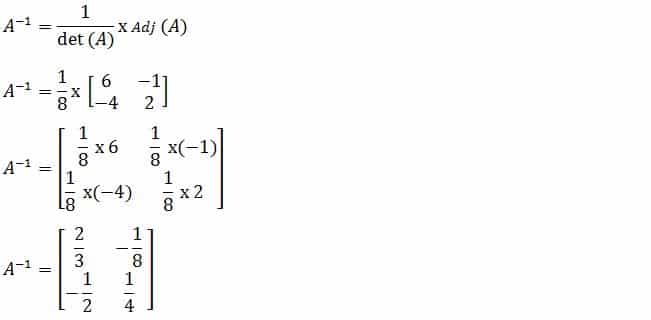
jawaban invers matriks

 

2. Invers matriks ordo 3 x 3 :

 

Rumus kebalikan dari matriks 3×3 sesuai dengan urutan 2×2 sebagai berikut :

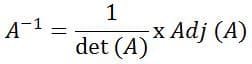
rumus invers matriks 3x3

Hampir seperti dalam pencarian perkalian dari matriks 2×2 di atas, pertama-tama kita harus menemukan determinan untuk menemukan matriks invers 3×3. Penentu urutan 3×3 dapat dicari dengan dua metode:

  1. Metode Sarrus
  2. Metode Minor – Kofaktor

Secara umum, determinan terbalik dari matriks 3×3 lebih mudah untuk dihitung menggunakan metode Sarrus. Metodenya adalah sebagai berikut :

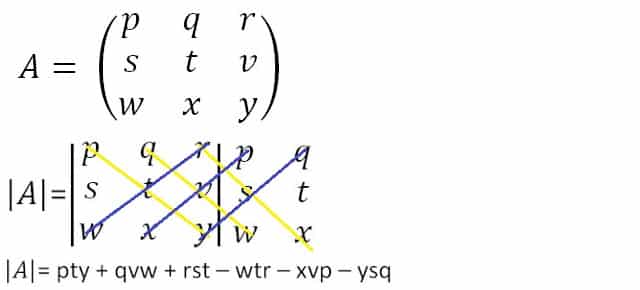
metode sarrus

Selanjutnya kita mencari matriks tetangga dalam rumus matriks terbalik. Untuk menghitung matriks yang berdekatan, pertama-tama kita perlu menentukan nilai matriks kofaktor.

Matriks kofaktor adalah matriks yang elemennya dimodifikasi oleh nilai-nilai determinan yang nilainya bukan kolom dan tidak selaras dengan elemen sumber.

Kemudian, sebagai alternatif, tanda positif atau negatif diberikan sebagai berikut :

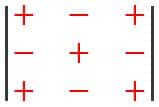
invers matriks 3x3

Jadi, Anda lebih memahami rumus invers dari matriks 3×3. Saya akan memberikan contoh masalah yang berkaitan dengan rumus terbalik ini. Berikut adalah contoh masalah matriks terbalik.

 

Contoh soal :

 

1. Matriks A dikenal sebagai berikut :

contoh soal matriks 3x3

 

Menentukan kebalikan dari matriks di atas A!

Jawaban :

jawaban matriks 3x3

 

 

 

 

Komentar

Posting Komentar

Postingan populer dari blog ini

PENERAPAN TURUNAN: KEMONOTONAN, INTERVAL FUNGSI NAIK/TURUN, KECEKUNGAN DAN UJI TURUNAN KEDUA

-
Gambar
Nama : Reinaldi Akmal (30) Kelas : XI IPS 2 PENERAPAN TURUNAN:  KEMONOTONAN, INTERVAL FUNGSI NAIK/TURUN, KECEKUNGAN DAN UJI TURUNAN KEDUA Kecekungan Karakteristik suatu fungsi yang naik atau turun dapat kita gunakan untuk mendeskripsikan grafik fungsi tersebut. Selain itu, apabila kita tahu dimana letak selang yang membuat f ’ naik atau turun maka kita dapat menentukan di mana grafik fungsi f akan cekung ke atas atau cekung ke bawah . Definisi Kecekungan Misalkan f terdiferensialkan pada selang buka I. Grafik f akan cekung ke atas pada I jika f ’ naik pada selang tersebut dan akan cekung ke bawah pada I jika f ’ turun pada selang tersebut. Interpretasi grafis kecekungan dari suatu fungsi berikut akan sangat berguna. Misalkan f terdiferensialkan pada selang buka I . Jika grafik f cekung ke atas pada I , maka grafik f berada di atas semua garis singgungnya pada selang tersebut. (Lihat gambar (a) di bawah). Misalkan f terdiferensialkan pada selang buka I . Jika grafik ...
Baca selengkapnya

Pengalaman Belajar Matematika dan soal Trigonometri (ReinaldiAkmal(31) X IPS 2)

-
Gambar
"Pengalaman Belajar Matematika dan soal Trigonometri" Reinaldi Akmal(31) X IPS 2  Assalamualaikum wr.wb, Perkenalkan , Saya Reinaldi Akmal absen (31) Kelas X IPS 2 dari SMAN 63 Jakarta Selatan. Tujuan pembuatan blog ini adalah untuk memenuhi tugas Matematika Pada hari selasa,28,april,2020. Puji dan Syukur kita panjatkan atas kehadirat ALLAH SWT. yang selalu memberikan kesehatan kepada kita sampai saat ini.             Pengalaman belajar Matematika SMAN 63 Jakarta Selatan,Oleh Reinaldi Akmal (31) X IPS 2 , Menurut Saya dalam pembelajaran matematika di semester 2 ini cukup sulit namun seiring waktu saya dapat mengikuti materinya dengan cukup baik. Dalam keadaan PSBB ini kegiatan KBM yang awalnya dilaksanakan disekolah mulai diganti sementara menjadi PJJ dirumah, meski banyak kendala dalam pembelajaran jarak jauh ini tapi saya selalu berusaha mengerjakan tugas yang diberikan tepat waktu.     ...
Baca selengkapnya