METODE PEMBUKTIAN DALAM MATEMATIKA
27 juli, 2020
Nama : Reinaldi Akmal (29)
Kelas : XI IPS 2
PEMBUKTIAN LANGSUNG
Pembuktian
langsung adalah metode pembuktian yang menggunakan alur maju. Mulai
dari pendefinisian sampai menghasilkan kesimpulan. Logika matematika sendiri mempelajari pernyataan yang bisa bernilai
benar atau salah, ekivalen atau ingkaran sebuah pernyataan, dan juga
berisi penarikan kesimpulan.
Buktikan bahwa jumlah dua bilangan ganjil adalah bilangan genap.
Bukti
Misalkan bilangan tersebut adalah m
dan n. Karena m dan n ganjil, maka terdapat bilangan bulat p dan q
sedemikian sehingga m=2p+1 dan n=2q+1. Dengan menjumlahkan diperoleh
m+n=(2p+1)+(2q+1)=2p+2q+2=2(p+q+1)=2k
Karena m+n=2k untuk bilangan bulat k=p+q+1 maka m+n merupakan bilangan genap berdasarkan definisi bilangan genap.
Q.E.D.
contoh soal :
1. Soal Jika diketahui nadalah ganjil, maka buktikan bahwa n2 adalah ganjil.
Diketahui n adalah ganjil, artinya terdapat suatu bilangan bulat k sehingga n = 2k+ 1.Akan ditunjukkan bahwa n2 ganjil. n2 = (2k+ 1)2= 4k2+ 4k+ 1= 2(2k2+ 2k) +1. Perhatikan bahwa n2= 2(2k2+ 2k) +1.Karena k adalah bilangan bulat, maka (2k2+ 2k) juga pasti bilangan bulat, sehingga n2 adalah ganjil.
2. Soal Jika diketahui m, nadalah kuadrat sempurna, maka buktikan bahwa mnadalah juga kuadrat sempurna
Misalkan m, nadalah kuadrat sempurna, artinyam= k2, n= p2, untuk suatu k, psuatu bilangan bulat.
mn = (k2)(p2)
= (kp)2
Karena k,p.
PEMBUKTIAN TIDAK LANGSUNG
yaitu bukti yang tidak mulai dari premis dari suatu teorema namun berakhir pada kesimpulan teorema tersebut. Kita tahu bahwa nilai kebenaran suatu implikasi p->q ekuivalen dengan nilai kebenaran kontraposisinya ->q->p. Jadi pekerjaan membuktikan kebenaran pernyataan implikasi dibuktikan lewat kontraposisinya.
Contoh Buktikan,
jika x2 bilangan ganjil maka x bilangan ganjil. Bukti. Pernyataan ini sangat sulit dibuktikan secara langsung. Mari kita coba saja. Karena x2 ganjil maka dapat ditulis x = 2m + 1 untuk suatu bilangan asli m. Selanjutnya x = 12m tidak dapat disimpulkan apakah ia ganjil atau tidak. Sehingga bukti langsung tidak dapat digunakan. Kontraposisi dari pernyataan ini adalah ”Jika x genap maka x2genap”.Selanjutnya diterapkan bukti langsung pada kontraposisinya. Diketahui x genap, jadi dapat ditulis x = 2n untuk suatu bilangan bulat n. Selanjutnya, x2 = (2n)2 = 2 (2n2) = 2m m yang merupakan bilangan genap.
1. Kontraposisi
Kontraposisi
adalah salah satu metode pembuktian tidak langsung. Kontraposisi
memanfaatkan salah satu prinsip dalam logika matematika yaitu

Artinya, kalau mau membuktikan
pernyataan p akan menghasilkan pernyataan q itu benar, maka buktikan
saja bila bukan q maka akan menghasilkan bukan p.
“Bila n bilangan bulat dan 7n + 9 bilangan genap, maka n bilangan ganjil”
Misalnya pernyataan p adalah 7n + 9 bilangan genap dan
pernyataan q adalah n bilangan ganjil. Maka yang kita buktikan adalah bila n bukan bilangan ganjil (bilangan genap), maka 7n + 9 bukan bilangan genap (bilangan ganjil).
Contoh : Buktikan bahwa: “jika n2 bilangan ganjil, maka n bilangan ganjil”.
Bukti : Untuk membuktikan pernyataan tersebut kita akan membuktikan
kebenaran kontraposisinya.
Misalnya : p = n2 bilangan
ganjil dan q = n bilangan ganjil
Apakah p → q benar ? Kita akan periksa apakah ~q → ~p benar ?
Andaikan n bukan bilangan ganjil, maka n bilangan genap, sehingga n dinyatakan dengan sebagai n = 2k, k bilangan asli.
Akibatnya n2 = (2k)2 = 4k2 = 2(2k2).
Artinya n2 bilangan genap.
Jadi pengandaian bahwa n bukan bilangan ganjil adalah BENAR,
sehingga kontraposisi ~q →~p juga BENAR.
Jadi implikasi p → q benar , ini berarti n2
bilanganganjil maka n adalah
bilangan ganjil.
2. Kontradiksi
kontradiksi adalah suatu pernyataan majemuk yang bernilai salah untuk semua kemungkinan dari premis-premisnya.Kontradiksi ini juga termasuk pembuktian tidak langsung.
Jika p → q bernilai benar padahal q salah, maka p salah
“Bila n bilangan bulat dan n bilangan genap maka 7n + 9 bilangan ganjil”
pernyataan p adalah n bilangan genap dan pernyataan q adalah 7n + 9
adalah bilangan ganjil. Maka dengan kontradiksi, kita buktikan , misalnya
pernyataan n bukan bilangan genap (bilangan ganjil) maka 7n + 9 adalah
bilangan ganjil benar, akan muncul suatu kontradiksi. Coba perhatikan gambar di bawah.
Contoh : Buktikan bahwa : “Untuk semua bilangan bulat n, jika n2 ganjil, maka n ganjil”.
Bukti : Andaikan bahwa q salah, atau ~q benar
yaitu n bukan bilangan bulat
ganjil, maka n bilangan bulat genap.
Dapat dimisalkan n = 2k dengan k bilangan bulat.
Dengan demikian maka n2 = (2k)2 atau n2 = 4k2
Ini menunjukkan
bahwa n2 =
bilangan bulat genap (~p)
Terjadilah suatu kontradiksi : yang diketahui p benar, sedangdari langkah-langkah logis diturunkan ~p benar.
Oleh karena itu kontradiksi tidak boleh terjadi, maka pengandaian harus diingkar yang berarti ~q salah atau q
benar.
contoh soal :
1. Misalkan himpunan A didefinisikan sebagai interval setengah terbuka A := [0,1). Buktikan maksimum A tidak ada. Bukti. Pernyataan ini dapat dinayatakan dalam bentuk implikasi berikut ”jika A := [0,1) maka maksimum A tidak ada.”
Andaikan maksimum A ada, katakan p. Maka haruslah 0 < p < 1, dan akibatnya p21< 21 dan 21(p + 1) < 1. Diperoleh p = p21 + p21 < p21 + 21 = 21(p + 1) < 1 Diperoleh dua pernyataan berikut : p maksimum A, yaitu elemen terbesar himpunan A. ada qA (yaitu q := 21(p + 1)) yang lebih besar dari p. Kedua pernyataan ini kontradiktif, jadi pengandaian A mempunyai maksimum adalah salah, jadi haruslah tidak ada maksimum.
Tidak ada bilangan bulat positif x dan y yang memenuhi persamaan Diophantine x2- y2 = 1.
Bukti. Misalkan ada bilangan bulat positif x dan y yang memenuhi x2- y2 = 1. Maka pada ruas kiri dapat difaktorkan sehingga diperoleh
Karena x, y bulat maka persamaan terakhir ini hanya dapat terjadi bilamana x - y = 1 dan x + y = 1 atau x - y = -1 dan x + y = -1. Pada kasus pertama akan dihasilkan x = -1 dan y = 0, sedangkan pada kasus kedua dihasilkan x = 1 dan y = 0. Hasil pada kedua kasus ini bertentangan dengan hipotesis bahwa x dan y bulat positif.
INDUKSI MATEMATIKA
Induksi matematika adalah materi yang jadi perluasan
dari logika matematika. Logika matematika mempelajari pernyataan yang
bisa bernilai benar maupun salah, ekivalen ataupun ingkaran sebuah
pernyataan, dan juga berisi penarikan kesimpulan.
Prinsip Induksi Matematika :
Misalkan P(n) adalah suatu pernyataan yang menyangkut
bilangan asli n.
Apabila P(1) benar, dan apabila P(k) benar maka P(k+1) juga benar, berakibat P(n) benar untuk
semua n.
Contoh : Buktikan bahwa : “1 + 3 + 5 + … +
(2n-1) = n2, untuk semua bilangan
asli n”.
Bukti : Misalkan P(n) adalah 1 + 3 + 5 + 7 + … +
(2n-1) = n2
P(1) benar, sebab 1 = 1
Bila P(k) benar, yaitu apabila ; 1 + 3 + 5 + 7 + … + (2k-1) = k2,
maka
1 + 3 + 5 + 7 + … + 2k-1 + 2k+1= (1 + 3
+ 5 + 7 + … + 2k- 1 + 2k+1.
= k2 + 2k + 1
= (k + 1)2
Sehingga P(k+1) benarLangkah – Langkah Induksi Matematika
Ada tiga langkah dalam induksi matematika yang dibutuhkan untuk membuktikan suatu rumus ataupun pernyataan. yaitu :
- pembuktian pada rumus ataupun pernyataan itu benar untuk n = 1
- pembuktian pada rumus ataupun pernyataan tersebut benar untuk n = k
- Membuktikan pada rumus ataupun pernyataan itu benar untuk n = k + 1
Contoh Soal Induksi Matematika
Buktikan bahwa :
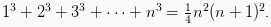
Langkah 1
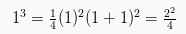
1 = 1 ( terbukti )
Langkah 2 ( n = k )
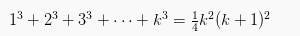
Langkah 3 (n=k+1)
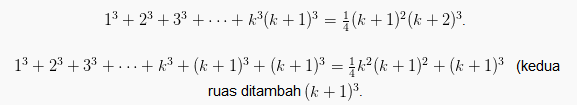
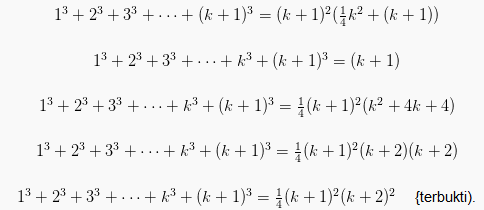
DAFTAR PUSTAKA

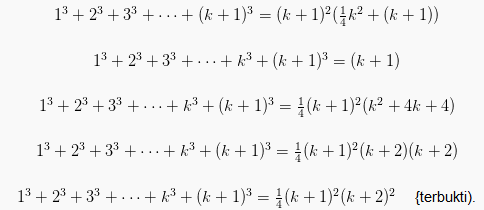
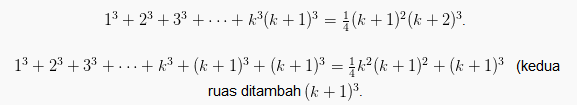


Komentar
Posting Komentar