REMEDIAL PAT SOAL TRIGONOMETRI MATEMATIKA REINALDI AKMAL (31) X IPS 2
- Dapatkan link
- X
- Aplikasi Lainnya
SOAL REMEDIAL PAT
NAMA : REINALDI AKMAL (31)
KELAS : X IPS 2
3.7 Menyelesaikan cara merubah satuan pengukuran sudut trigonometri radian ke derajat, derajat ke radian
Soal :
1.Ubahlah sudut-sudut berikut dalam derajat
a. π3 rad = ... °
b. 4π rad = ... °
Jawab :
a. π3 rad = π3 . 180∘π = 60°
b. 4π rad = 4π . 180∘π = 720°
Soal :
1.Ubahlah sudut-sudut berikut dalam derajat
a. π3 rad = ... °
b. 4π rad = ... °
Jawab :
a. π3 rad = π3 . 180∘π = 60°
b. 4π rad = 4π . 180∘π = 720°
3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku dan dudut istimewa (600 , 300 , 450 )
soal : 1.
Penyelesaian :


Kalikan dengan akar sekawan:





*). Fungsi awal :f(x)=−x2+4x+3
f′(x)=−2x+4 dan f′′(x)=−2
*). Menentukan nilaix dari syarat stasioner : f′(x)=0
f′(x)=0→−2x+4=0→x=2 .
*). Menentukan jenis stasionernya : gunakan turunan kedua.
untukx=4→f′′(2)=−2 (negatif), jenisnya maksimum. Artinya nilai x=2 menyebabkan fungsinya maksimum.
*). Menentukan nilai maksimum saatx=2 , substitusi ke fungsi awal
fmaks=f(2)=−(2)2+4.2+3=7
Jadi, nilai maksimum fungsif(x)=−x2+4x+3 adalah 7 pada saat x=2 .
2). Tentukan nilai minimum fungsif(x)=13x3+12x2−2x+3 ?
Penyelesaian :
*). Fungsi awal :f(x)=13x3+12x2−2x+3
f′(x)=x2+x−2 dan f′′(x)=2x+1
*). Menentukan nilaix dari syarat stasioner : f′(x)=0
f′(x)=0→x2+x−2=0→(x+2)(x−1)=0→x=−2∨x=1 .
*). Menentukan jenis stasionernya : gunakan turunan kedua.
untukx=−2→f′′(−2)=2.(−2)+1=−3 (negatif), jenisnya maksimum. Artinya nilai x=−2 menyebabkan fungsinya maksimum.
untukx=1→f′′(1)=2.(1)+1=3 (positif), jenisnya minimum. Artinya nilai x=1 menyebabkan fungsinya minimum.
*). Menentukan nilai minimum saatx=1 , substitusi ke fungsi awal
fmin=f(1)=13.13+12.12−2.1+3=116
Jadi, nilai maksimum fungsif(x)=13x3+12x2−2x+3 adalah 116 pada saat x=1 .
soal : 1.
Pada gambar di samping segitiga siku-siku ABC dengan panjang a=8 dan c= 10.
Tentukan keenam perbandingan trigonometri untuk a.
Penyelesaian:
Nilai b dihitung dengan teorema Pythagoras
3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku di dalam koordinat kartesius

Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni −30∘.
Karena satu putaran sama dengan 360∘, maka −30∘ sama dengan (360−30)∘=330∘
Jadi, besar sudutnya adalah 330∘
soal :
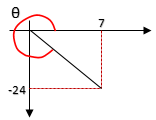
1. Besar sudut yang sesuai dengan gambar di bawah adalah ⋯⋅

Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni −30∘.
Karena satu putaran sama dengan 360∘, maka −30∘ sama dengan (360−30)∘=330∘
Jadi, besar sudutnya adalah 330∘
jawab :
x=7, y=−24, r=25 (Phytagoras) Koordinat Cartesius → cos=absis/radius
cosθ =x/r=725
3.7 Menyelesaikan komposisi operasi (+, -, :, dan •) nilai trigonometri
Contoh Soal 1
Tentukanlah nilai berikut ini.
a. cos 120º sin 60º
b. sin 75º cos 15º
Jawab
a. cos 120º sin 60º = ½ (sin (A + B) - sin (A - B))
= ½ (sin (120º + 60º) - sin (120º - 60º))
= ½ (sin (180º) - sin (60º))
= ½ (0 - ½√3)
= ½ (-½√3)
= -¼√3
b. sin 75º cos 15º = ½ (sin (A + B) + sin (A - B))
= ½ (sin (75º + 15º) + sin (75º - 15º))
= ½ (sin (90º) + sin (60º))
= ½ (1 + ½√3)
= ½ + ¼√3
3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran
soal :
1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20°
tan 40°
cos 53°
Jawab :
sin 20° = sin (90° − 70°)
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50°
cos 53° = cos (90° − 37°)
= sin 37°
3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut berelasi (kuadrat: I, II, III, IV), sudut negatif, dan sudut > 3600
soal :
sin 233°
cos 323°
Jawab :
Sudut 143° terletak pada kuadran II, sehingga tan 143° bernilai negatif.
tan 143° = tan (180° − 37°)
tan 143° = -tan 37°
Sudut 233° terletak pada kuadran III, sehingga sinus bernilai negatif.
sin 233° = sin (270° − 37°)
tan 233° = -cos 37°
Perhatikan bahwa sin berubah menjadi cos karena relasi yang digunakan (270° − α)
Sudut 323° terletak pada kuadran IV, sehingga cosinus bernilai positif.
cos 323° = cos (360° − 37°)
cos 323° = cos 37°
soal :
1. Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20°
tan 40°
cos 53°
Jawab :
sin 20° = sin (90° − 70°)
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50°
cos 53° = cos (90° − 37°)
= sin 37°
3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut berelasi (kuadrat: I, II, III, IV), sudut negatif, dan sudut > 3600
soal :
1. Nyatakan setiap perbandingan trigonometri berikut dalam sudut 37° !
tan 143°sin 233°
cos 323°
Jawab :
Sudut 143° terletak pada kuadran II, sehingga tan 143° bernilai negatif.
tan 143° = tan (180° − 37°)
tan 143° = -tan 37°
Sudut 233° terletak pada kuadran III, sehingga sinus bernilai negatif.
sin 233° = sin (270° − 37°)
tan 233° = -cos 37°
Perhatikan bahwa sin berubah menjadi cos karena relasi yang digunakan (270° − α)
Sudut 323° terletak pada kuadran IV, sehingga cosinus bernilai positif.
cos 323° = cos (360° − 37°)
cos 323° = cos 37°
3.8 Menyelesaikan persamaan trigonometri sederhana atau persamaan indentitas trigonometri = rumus identitas trigonometri
Contoh Soal 1
Jika cos2A=−725 untuk 180∘≤2A≤270∘, maka ⋯⋅
Diketahui cos2A=−7/25.
Karena 180∘≤2A≤270∘, maka dengan membagi 2 pada ketiga ruasnya, diperoleh
90∘≤A≤135∘.
Jadi, A berada di kuadran II.
Perhatikan bahwa cos2A=2cos2A−1.
cos2A=−7/25
Karena 180∘≤2A≤270∘, maka dengan membagi 2 pada ketiga ruasnya, diperoleh
90∘≤A≤135∘.
Jadi, A berada di kuadran II.
Perhatikan bahwa cos2A=2cos2A−1.
cos2A=−7/25
2cos2A−1=−7/25
cos2A=9/25
cosA=−35
cosA bernilai negatif karena A berada di kuadranII
segitiga siku-sikutanAcosA bernilai negatif karena A berada di kuadranII
cscA=mi/de=5/4
3.8 Menyelesaikan Koordinat kutub ke koordinat kartesius, koordinat kartesius ke koordinat kutub
Contoh Soal 1
Konversikan koordinat kartesius P (4,-3) menjadi koordinat kutub!
Penyelesaian:
Diketahui: x = 4 dan y = -3
Penyelesaian:
Diketahui: x = 4 dan y = -3
maka r = √x²+y² = √4²+(-3)² = √25 = 5
α = tan^-1 (y/x) = tan^-1 (-3/4)
= -36,69 ° atau -37°
Jadi koordinat kutubnya (5, -37°).
= -36,69 ° atau -37°
Jadi koordinat kutubnya (5, -37°).
3.8 Menyelesaikan soal cerita perbandingan trigonometri
Contoh Soal 1
Perhatikan gambar di bawah!
Sisno diminta mengukur tinggi tiang bendera menggunakan klinometer. Saat pertama berdiri dengan melihat ujung tiang bendera, terlihat pada klinometer menunjuk pada sudut 60o. Kemudian ia bergerak menjauhi tiang bendera sejauh 10 meter dan terlihat pada klinometer sudut 45o. Tinggi tiang bendera adalah ….
Penyelesaian :
Perhatikan ilustrasi berikut.
Mencari nilai t:


Mencari nilai x:
Kalikan dengan akar sekawan:


Jadi, tinggi tiang bendera (t) adalah


3.9 Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi
Contoh Soal 1
Diketahui segitiga ABC dengan ∠A = 45°,∠B = 30° dan panjang AC = 6. Tentukan panjang BC !
Jawab :
Jawab :
BCsin45∘=6sin30∘
BC = 6×sin45∘sin30∘
BC = 6×12√212
BC = 6√2
Jadi, panjang BC adalah 6√2
BC = 6×sin45∘sin30∘
BC = 6×12√212
BC = 6√2
Jadi, panjang BC adalah 6√2
3.9 Menyelesaikan aturan sinus diketahui 1 sudut dan 2 sisi
Contoh Soal 1
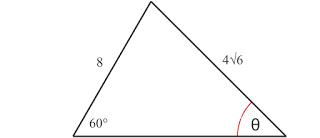
Tentukan besar sudut θ dari segitiga berikut
Jawab :
8sinθ=4√6sin60∘
sin θ = 8×sin60∘4√6
sin R = 8×12√34√6 (rasionalkan)
sin R = 12√2
⇒ θ = 45°
Jadi, besar sudut θ adalah 45°
sin θ = 8×sin60∘4√6
sin R = 8×12√34√6 (rasionalkan)
sin R = 12√2
⇒ θ = 45°
Jadi, besar sudut θ adalah 45°
3.9 Menyelesaikan aturan cos ditanya sisi
Contoh Soal 1
Tentukan x dari segitiga berikut !
Jawab :
Dengan aturan cosinus :
x2 = 42 + 62 − 2. 4. 6. cos 60°
x2 = 42 + 62 − 2. 4. 6. 12
x2 = 28
x = √28 = 2√7
Jadi, nilai x adalah 2√7
Dengan aturan cosinus :
x2 = 42 + 62 − 2. 4. 6. cos 60°
x2 = 42 + 62 − 2. 4. 6. 12
x2 = 28
x = √28 = 2√7
Jadi, nilai x adalah 2√7
3.9 Menyelesaikan aturan cos ditanya sudut
Contoh Soal 1
Diketahui segitiga PQR dengan PQ = 2√3, QR = 1 dan PR = √7. Jika ∠Q = θ, tentukan θ!
Jawab :
Dengan aturan cosinus :
(√7)2 = (1)2 + (2√3)2 − 2. 1. 2√3. cos θ
7 = 1 + 12 − 4√3. cos θ
4√3. cos θ = 6
cos θ = 64√3 (rasionalkan)
cos θ = 12√3
⇒ θ = 30°
atau
cos θ = 12+(2√3)2−(√7)22.1.2√3
cos θ = 1+12−74√3
cos θ = 64√3 (rasionalkan)
cos θ = 12√3
⇒ θ = 30°
(√7)2 = (1)2 + (2√3)2 − 2. 1. 2√3. cos θ
7 = 1 + 12 − 4√3. cos θ
4√3. cos θ = 6
cos θ = 64√3 (rasionalkan)
cos θ = 12√3
⇒ θ = 30°
atau
cos θ = 12+(2√3)2−(√7)22.1.2√3
cos θ = 1+12−74√3
cos θ = 64√3 (rasionalkan)
cos θ = 12√3
⇒ θ = 30°
3.9 Menyelesaikan Luas segitiga jika diketahui: 1 sudut 2 sisi, 3 sisi, 2 sudut 1 sisi
Contoh Soal 1
Segitiga ABC dengan ukuran diperlihatkan gambar diatas.
Tentukan luas segitiga!
Tentukan luas segitiga!
Pembahasan
Satu sudut diketahui beserta dua sisi pengapitnya, gunakan rumus dari kelompok 2.
Satu sudut diketahui beserta dua sisi pengapitnya, gunakan rumus dari kelompok 2.
3.10 Menyelesaikan gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Contoh Soal 1
Grafik fungsi f(x)=−2cos3x,−π≤x≤π adalah⋯⋅
Bentuk umum fungsi cosinus adalah f(x)=acos kx. Oleh karena f(x)=−2cos3x, makaa=−2 dan k=3.
Amplitudo grafiknya adalah −(−a)=a=2 dan saat x=0∘, nilai fungsinya adalahf(0)=−2cos3(0)=−2(1)=−2,
sehingga pilihan B, D, E tereliminasi.
Karena k=3, maka periode fungsinya adalah
k=2π/Periode
Amplitudo grafiknya adalah −(−a)=a=2 dan saat x=0∘, nilai fungsinya adalahf(0)=−2cos3(0)=−2(1)=−2,
sehingga pilihan B, D, E tereliminasi.
Karena k=3, maka periode fungsinya adalah
k=2π/Periode
3=2π/Periode⇔Periode=2/3π
periode grafiknya dapat dilihat dengan observasi berikut: dari titik x=0 ke titik x=π terdapat 1,5 gelombang (1,5 lembah; 1,5 bukit), sehingga periodenya adalah π−01,5=23π
Jadi, grafik fungsi f(x)=−2cos3x adalah
periode grafiknya dapat dilihat dengan observasi berikut: dari titik x=0 ke titik x=π terdapat 1,5 gelombang (1,5 lembah; 1,5 bukit), sehingga periodenya adalah π−01,5=23π
Jadi, grafik fungsi f(x)=−2cos3x adalah
3.10 Menyelesaikan membaca gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Contoh Soal 1
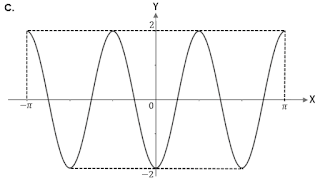
Fungsi yang sesuai dengan grafik berikut adalah ⋯⋅
Beranjak dari grafik sinus: karena kurvabergeser (ke kiri) sejauh π2, maka bentuk umum grafik fungsinya adalahf(x)=y=asink(x−c).
Untuk grafik ini, nilai c yang menentukan pergeseran kurva adalah −π2 (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik x=−π2 yang nilai fungsinya 0, grafik fungsi kembali bernilai0 dan berulang kembali di titik x=3π/2, sehingga periode grafik fungsinya adalah3π/2–(−π/2)=2π.
Dengan demikian,
k=2π/Periode=2π/2π=1
Nilai a ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum/2=2−(−2)/2=2
Untuk grafik ini, nilai c yang menentukan pergeseran kurva adalah −π2 (tandanya negatif, karena grafik bergeser ke kiri).
Dimulai dari titik x=−π2 yang nilai fungsinya 0, grafik fungsi kembali bernilai0 dan berulang kembali di titik x=3π/2, sehingga periode grafik fungsinya adalah3π/2–(−π/2)=2π.
Dengan demikian,
k=2π/Periode=2π/2π=1
Nilai a ditentukan oleh nilai maksimum dan nilai minimum fungsi, yakni
a=N. Maksimum−N. Minimum/2=2−(−2)/2=2
Jadi, rumus grafik fungsinya adalahf(x)=2sin1(x+π2)=2sin(x+π2)
3.10 Menyelesaikan Range nilai fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
Contoh Soal 1
Carilah turunan f'(x) dari fungsi-fungsi trigonometri dibawah ini :
a. f(x) = 4 sin x
b. f(x) = 3 cos x
c. f(x) = -2 cos x
d. f(x) = 2 sec x
e. f(x) = 2 csc x
Pembahasan
a. f(x) = 4 sin x
b. f(x) = 3 cos x
c. f(x) = -2 cos x
d. f(x) = 2 sec x
e. f(x) = 2 csc x
Pembahasan
a. f(x) = 4 sin x → f'(x) = 4 cos x
b. f(x) = 3 cos x → f'(x) = -3 sin x
c. f(x) = -2 cos x → f'(x) = -2 (-sin x) → f'(x) = 2 sin x
d. f(x) = 2 sec x → f'(x) = 2 sec x . tan x
e. f(x) = 2 csc x → f'(x) = 2 (-csc x . cos x) → f'(x) = -2 csc x . cot x
b. f(x) = 3 cos x → f'(x) = -3 sin x
c. f(x) = -2 cos x → f'(x) = -2 (-sin x) → f'(x) = 2 sin x
d. f(x) = 2 sec x → f'(x) = 2 sec x . tan x
e. f(x) = 2 csc x → f'(x) = 2 (-csc x . cos x) → f'(x) = -2 csc x . cot x
3.7 Menyelesaikan sudut elevasi, sudut depresi
soal :

3.10 Menyelesaikan fungsi trigonometri dengan menggunakan lingkaran satuan untuk menentukan periode maksimum dan minimum
soal :
1). Tentukan nilai maksimum dari fungsi f(x)=−x2+4x+3 ?
Penyelesaian : *). Fungsi awal :
*). Menentukan nilai
*). Menentukan jenis stasionernya : gunakan turunan kedua.
untuk
*). Menentukan nilai maksimum saat
Jadi, nilai maksimum fungsi
2). Tentukan nilai minimum fungsi
Penyelesaian :
*). Fungsi awal :
*). Menentukan nilai
*). Menentukan jenis stasionernya : gunakan turunan kedua.
untuk
untuk
*). Menentukan nilai minimum saat
Jadi, nilai maksimum fungsi
- Dapatkan link
- X
- Aplikasi Lainnya





















Komentar
Posting Komentar